Zu je zwei ganzen Zahlen n, m gibt es eine eindeutig bestimmte ganze Zahl q und – falls nicht ohnedies
gilt – eine eindeutig bestimmte ganze Zahl r < m mit
Es ist klar, dass aus die
Beziehung
aus der Vorstellung entsteht, beide Seiten der Gleichung werden durch m dividiert. Schreibt man statt r : m die Reihenfolge umgekehrt, kann man wegen r < m den Divisionsprozess für m und r wiederholen. Man setzt daher symbolisch:
Bei der Division m : r bestehen wieder beide
Möglichkeiten 
, wenn r Teiler von m
ist, oder 
mit
,
was in der obigen Symbolik entweder
oder
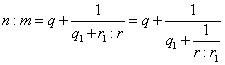
liefert. Diese Kettendivision kann so lange fortgeführt werden, bis eine Division ohne Rest ihren Abbruch herbeizwingt.
(è Bsp: 917:700)
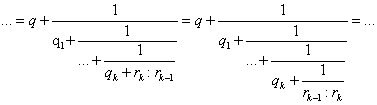
Wie man, sieht werden hier der Reihe nach die folgenden Divisionen durchgeführt:
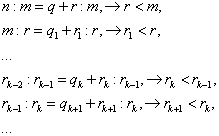
Da die Ungleichungskette
in 
nur endlich viele Reste zwischen
m und 1 zulässt, muss das Kettendivisionsverfahren einmal dadurch zu
Ende kommen, dass der letzte Rest – er sei 
genannt – den vorletzten
Rest 
teilt:
(bei k = 1 ist 
). Wegen 
muss 
sein und wir
erhalten:
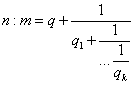
(è Bsp: Wurzel aus 2 und 40:7 in etwas anderer Schreibweise)
Schreiben wir das Kettendivisionsverfahren in umgekehrter Reihenfolge als
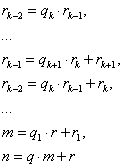
an und gehen wir davon aus, 
und 
wären beide
durch die natürliche Zahl d teilbar, dann zeigen diese Zeilen, dass d
auch die Zahlen und , sowie die Zahlen und teilt, was
sich schrittweise schließlich auf die Teilbarkeit von m und n
durch d überträgt. Genauso kann die Überlegung in Gegenrichtung gedacht
werden: eine gemeinsamer Teiler d von n und m ist auch
ein gemeinsamer Teiler von m und r, von r und r1
und so weiter.
Die erste Zeile zeigt offenkundig, dass 
der größte
gemeinsame Teiler von und ist; darum erweist sich
diese Zahl zugleich als der größte gemeinsame Teiler von n und m,
in Symbolen:
.
Im Falle d = 1 nennen wir die natürlichen Zahlen n und m relativ prim.
Sind n und m mit n > m > 1 zueinander relativ prime natürliche Zahlen und definiert man bei
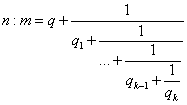
die zueinander relativ primen natürlichen Zahlen s und r gemäß
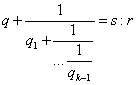
(bei s : r fehlt der letzte Teilnenner), dann gilt für ungerade k
und für gerade k
Euklid folgert hieraus:
Zu je zwei zueinander relativ primen natürlichen Zahlen n und m kann man natürliche Zahlen x und y mit
bestimmen.
(è Bsp: 
)
Zweitausend Jahre nach Euklid entdeckte Gauß bereits als junger Mann, dass eine bemerkenswerte Struktur der natürlichen Zahlen mit diesen Gleichungen verbunden ist. Gauß betrachtete neben der gewöhnlichen Gleichheit zwischen natürlichen Zahlen einen neue Gleichheitsrelation, die er Kongruenzen nannte: Ist m eine vorgegebene natürliche Zahl, wird die nicht durch m teilbare natürliche Zahl n > m mit dem Rest r identifiziert, den die Division von n und m ergibt:
gelesen als n ist zu r modulo m kongruent, bedeutet
Ist n durch m restlos teilbar, schreibt Gauß
Allgemein heißen zwei beliebige natürliche Zahle n
und r modulo der natürlichen Zahl m, des sogenannten Moduls,
wenn entweder n = r ist oder n < r die Differenz
bzw. bei 
die Differenz 
durch m
teilbar ist. Es ist klar, dass mit
und 
auch
stimmt und man kann ohne weiteres bestätigen, dass aus
und 
die Beziehung
und
folgen.
(èBsp: Kurzbeweis)
Fasst man mit Gauß die Kongruenzen nach dem Modul m als Gleichheitsbeziehung auf, nennt man die natürlichen Zahlen Restklassen modulo m. Es gibt genau m Restklassen modulo m von jeweils einander kongruenten Zahlen: die Nullklasse 0, welche zu allen durch m teilbaren Zahlen kongruent ist (und für m = 1 die einzige Restklasse ist – in diesem [trivialen] Fall sind alle natürlichen Zahlen zueinander kongruent), für m > 1 die Einsklasse 1, die zu allen Zahlen natürlichen Zahlen kongruent ist, die bei Division durch m den Rest 1 lassen, und so weiter bis zur (m – 1) – Klasse m – 1, zu der eine natürliche Zahl dann kongruent ist, wenn bei ihrer Division durch m der maximale Rest m – 1 verbeibt.