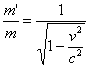Spezielle Relativitätstheorie

·          Berechnung des „Gamma“ Faktors

Aus der Lorentztransformation entnimmt man:

 und

Mit

folgt

und somit für die („ruhende“) Zeit

Einsetzen in die obige Gleichung ergibt

nun durch  dividieren und mit c multiplizieren. Es folgt

Umformen ergibt

und weiter

und

somit

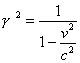
und schließlich die Wurzel ziehen:

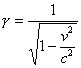
·          Berechnung der Zeitdilatation

            der ruhende Beobachter erkennt

Mit dem Satz von Pythagoras folgt

und damit

Herausheben von t und Division durch c ergibt

Ziehen der Quadratwurzel

oder

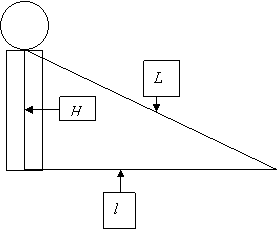
·          Berechnung der Längenkontraktion

Für die Längen(enden) gilt

Da die Messung im Bezugssystem gleichzeitig erfolgt (anlegen eines Maßstabes) gilt

 und Subtrahieren der 2. Gleichung von der 1. erbringt

mit

folgt

·          Berechnung der Transformationsgleichungen für die Zeit

mit den Transformationsgleichungen

folgt nach gegenseitigem Einsetzen

Division durch  ergibt                       

Trennung der gestrichenen von den ungestrichenen Größen

und erneut Division durch  ergibt      

somit                                                  

und damit                                           

x fällt heraus, Division durch v und Multiplikation mit  ergibt schließlich

Würde man die selbe Rechnung mit t durchführen ergäbe es:

·          Berechnen der Geschwindigkeitsaddition

Mit

und

folgt für

somit

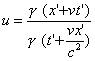
Division durch  und  ergibt

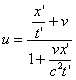
Da gilt , folgt nunmehr

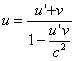
·          Beispiele

I.) Der nächste Fixstern ist Alpha-Centauri am südlichen Sternenhimmel. Seine Entfernung beträgt 4,5 Lichtjahre.

a) Wie lange bräuchte ein Raumschiff, um zum Stern und wieder zur Erde zu gelangen, wenn seine Geschwindigkeit  beträgt?

Mit

b)Wie lange würde der Flug für die Astronauten an Bord des Raumschiffes dauern?

Mit a

c) Welche Geschwindigkeit müsste das Raumschiff haben, damit für die Besatzung während der Reise nur ein Jahr vergeht?

Mit

II.) Ein Astronaut tritt mit 25 Jahren eine Weltraumreise an, die ihn mit  durch das All führt. Bei der Rückkehr ist sein Zwillingsbruder 69 Jahre alt. Wie alt ist der Astronaut?

Mit

III.) Ein Myon werde in 20 km Höhe durch die Höhenstrahlung erzeugt. Mit der Geschwindigkeit  fliegt es zur Erde. Wie stark ist im Ruhsystem der Myonen die Höhe H kontrahiert?

Mit  folgt

IV.) Auf das Wievielfache erhöht sich die Masse eines Körpers, wenn seine Geschwindigkeit a) 90%, b) 99% und c) 99,99% der Lichtgeschwindigkeit beträgt?

a)

b)

c)
Berechnung der Massenzunahme

Die Geschwindigkeit von einem bewegten System aus ist gegeben durch

Da aber  senkrecht auf v des Beobachters steht, gibt es keine Längenkontraktion und man schreibt

Für  gilt jedoch  und damit folgt

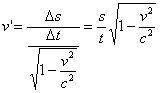
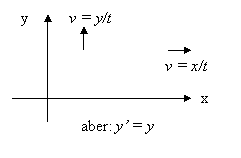
Und weil  folgt

Der Impulssatz lautet

somit folgt also

und damit (nach Division durch v)

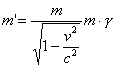
Für das konkrete Beispiel folgt also