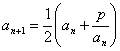Was ist ?

Man überlegt sich:

 und , also sollte die Zahl  zwischen den Zahlen  und  liegen.

Man überlegt weiter:

Das kann man aber auflösen zu:

und

weiters

 herausheben

und schließlich durch  dividieren

Nun kann man  beliebig oft einsetzen und berechnen:

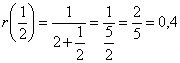
und

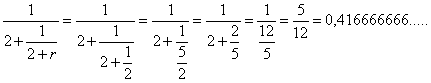
und

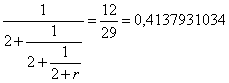
und mit beliebiger Genauigkeit:

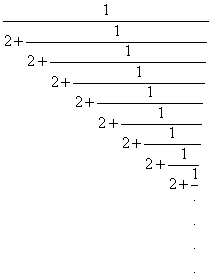
Der Wert von  auf 9 Stellen genau berechnet beträgt:

Dies nennt man einen Kettenbruch.

Mit seiner Hilfe kann jede Wurzel einer ganzen Zahl, als ein stetiger Bruch dargestellt  und somit beliebig genau berechnet werden. Die Methode wurde zuerst von den Babyloniern entdeckt. Außerdem dient er als „Beweis“ für die Irrationalität einer Zahl, da jede rationale Zahl einmal mit Null-Rest den Kettenbruch abbricht. Und schließlich wurde diese Art der Rechnung vom Griechen Euklid benutzt um den größten gemeinsamen Teiler zweier beliebiger Zahlen zu berechnen. Später wurde diese Methode erweitert und diente zur Berechnung des ggT von zwei oder mehr  Polynomen! Man nennt Euklid zu Ehren, den Kettenbruch auch „Euklidschen Algorithmus“.

Berechne mit Hilfe des Kettenbruches die !

Hat man einmal mit dem Kettenbruch gerechnet, so merkt man, dass man ja nicht jedes mal die ganze Serie rechnen muss. Durch einiges überlegen und geschicktes umformen findet man eine Rekursionsformel. Das bedeutet, dass jedes mal der berechnete Wert in die Formel eingesetzt wird um einen neuen Wert zu erhalten, der dann wieder eingesetzt wird, und so fort...

Eine allgemeine Formel für die  lautet: