Die Exponentialfunktion
Um 1740 von Euler begründet und erstmals den Buchstaben „e“ eingeführt für die „natürliche Exponantialfunktion“
Aus der Gleichung
![]()
schließt man auf die Relation
![]()
für unendlich kleine ![]() . Dabei sei aus
Stetigkeitsgründen
. Dabei sei aus
Stetigkeitsgründen ![]() wieder eine unendlich kleine
Zahl. Man setzt
wieder eine unendlich kleine
Zahl. Man setzt ![]() .
. ![]() ist demnach der Logarithmus
von
ist demnach der Logarithmus
von ![]() zur
Basis a
zur
Basis a
![]()
Ein Beispiel zeigt, daß die Zahl k von der
Basis a abhängt: für ![]() und
und ![]()
![]() ist
ist
![]()
k ist also eine endliche Zahl. Jetzt bildet man die i-te Potenz auf beiden Seiten der Gleichung
![]()
und entwickelt davon die rechte Seite nach dem binomischen Lehrsatz
![]()
i ist dabei eine beliebige Zahl. Setzt man:
![]() , wobei z irgend eine endliche
Zahl bedeutet, so wird, da
, wobei z irgend eine endliche
Zahl bedeutet, so wird, da ![]() unendlich klein ist, also i
unendlich groß sein. Einsetzen von
unendlich klein ist, also i
unendlich groß sein. Einsetzen von ![]() für
für ![]() führt auf
führt auf
![]()
Dies ist eine Gleichung für die endliche Potenz
![]() , bei der auf der rechten Seite aber
leider noch die unendlich großen Zahlen
, bei der auf der rechten Seite aber
leider noch die unendlich großen Zahlen ![]() stehen.
stehen.
Jetzt argumentiert man, daß für unendlich große Zahlen i gilt:
![]()
und entsprechend
![]()
![]()
![]()
Damit wird die Reihe zu
![]()
und weiters
![]()
Zur Herleitung einer Reihe für den Logarithmus setzt man nun
![]()
weil
![]()
Daraus folgt
![]()
Wieder wird die rechte Seite in einer Binomialreihe
entwickelt und man gewinnt eine Reihe für ![]()
![]()
mit der obigen Vereinfachung folgt
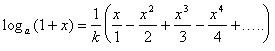
Dies wird besonders einfach für ![]() . Für diesen Wert
bezeichnet man die Basis mit dem Buchstaben e
. Für diesen Wert
bezeichnet man die Basis mit dem Buchstaben e
![]()
insbesondere gilt für die Basis e
![]()
Euler berechnet die Basis e der „natürlichen Logarithmen“ auf 23 Stellen:
![]()
Die Reihe für ![]() sieht dann so aus:
sieht dann so aus:
![]()
Euler findet noch die wichtige Formel
![]()
für unendlich großes i. Sie entspricht der modernen Darstellung
![]()
ganz allgemein hat die Exponentialfunktion die Form:
![]()
Anwendungen in den Naturwissenschaften
Wachstumsfunktionen
z.B.: des Waldes
Baumbestand nimmt jährlich um p % zu, daher multupliziert sich das Volumen jährlich mit
![]()
wird nicht geschlägert, gilt
![]()
z.B.: von Bakterien
Sind ![]() Bakterien in Nährlösung,
vergeht zwischen aufeinanderfolgenden Teilungen im Mittel die Zeit
Bakterien in Nährlösung,
vergeht zwischen aufeinanderfolgenden Teilungen im Mittel die Zeit ![]() (Verdopplungszeit),
gilt
(Verdopplungszeit),
gilt
![]()
z.B.:Abnahme des Luftdruckes
Luftdruck nimmt mit zunehmender Höhe ab und zwar sinkt er jeweils um die Hälfte, wenn die Höhe um etwa 5,5 km zunimmt
![]()
z.B.: gedämpfte Schwingungen
Durch Reibung nimmt Amplitude ab, mit konstantem
Faktor q (q < 1). Nach n Schwingungen ist Amplitude
mit Ausgangswert ![]() auf den Wert a gesunken
auf den Wert a gesunken
![]()
z.B.: Absorbtion von Licht
Verliert Licht beim Durchgang durch ein durchsichtiges Material der Dicke h die Hälfte seiner Intensität, nach der nächsten Schicht wieder und so fort, gilt nach der Schichtdicke x
![]()
Zerfallsfunktion:
radioaktiver Zerfall:
Die Zeit, in der von einem vorhandenen Quantum die Hälfte zerfällt, heißt Halbwertszeit.
![]()
Skizze eines Beispiels:
Wachstum
![]() Anzahl der Menschen zur Zeit
t und r der Unterschied zwischen Geburten- und Sterberate, dann
Anzahl der Menschen zur Zeit
t und r der Unterschied zwischen Geburten- und Sterberate, dann
![]()
Die Änderung der Bevölkerung pro Zeiteinheit. Im
einfachsten Fall ist r = konst. Dies ist das mathematische Modell für
das Malthussche Bevölkerungsgesetz. Da man weiß, wieviel Menschen zur Zeit
![]() 1950 gelebt haben, gilt außerdem
1950 gelebt haben, gilt außerdem ![]() (Anfangswertproblem).
(Anfangswertproblem).
Die Lösung ist dann:
![]()
Ist die Anzahl sehr groß, fällt die Zunahme um ein paar Menschen nicht ins Gewicht, daher bleibt die Funktion stetig. Bleibt die Frage ob so ein Modell sinnvoll ist. r erhält man, indem man mit zwei reellen Werten vergleicht: Für 1950 und 1970 erhält man in Mio gemessen
![]()
und damit
![]()
Jahr
1
1850
1940
1950
1960
1970
1980
1990
ca.160
ca.1200
2249
2509
3010
3632
4419
5,5 10-13
395
2085
2509
3019
3632
4371
5259
nur für „kleine“ Zeiträume genau! Laut der Formel können im Jahr 1 überhaupt keine Menschen gelebt haben. Im Jahr 2700 würden dagegen etwa 2 662 788 041 Mio Menschen leben
1837 holländischer Biomathematiker stellt das „logistische Gesetz“ des Populationswachstums auf:
![]()
![]() sind positive Konstanten.
sind positive Konstanten. ![]() umso kleiner,
je größer der dem einzelnen Exemplar zur Verfügung stehende Lebensraum und je
mehr Nahrungsmittel.
umso kleiner,
je größer der dem einzelnen Exemplar zur Verfügung stehende Lebensraum und je
mehr Nahrungsmittel. ![]() ein Erfahrungswert, der heute zu
ein Erfahrungswert, der heute zu ![]() berechnet
wird.
berechnet
wird. ![]() können
durch verbesserte medizinische Betreuung, technologische Entwicklungen, Naturkatstrophen,
Umweltverschmutzung, etc. beeinflußt werden. Man kann viele Verbesserungen einbauen,
langfristig bleibt es sehr fragwürdig.
können
durch verbesserte medizinische Betreuung, technologische Entwicklungen, Naturkatstrophen,
Umweltverschmutzung, etc. beeinflußt werden. Man kann viele Verbesserungen einbauen,
langfristig bleibt es sehr fragwürdig.
Mit ![]() findet man:
findet man:
![]()
Wird t immer größer, nähert sich der Quotient
immer mehr dem Ausdruck ![]() , also
, also
![]()
Mit anderen Worten, die Zuwachsrate strebt den Wert
Null an. Mit obigem ![]() ergibt sich für
ergibt sich für ![]()
![]()
und damit die Erdbevölkerung zu
![]() Milliarden Menschen.
Milliarden Menschen.