Man denkt sich die Geschwindigkeitsvektoren der Teilchen in ihre Komponenten in die 6 Richtungen der Koordinatenachsen (positive und negative x-, y-, und z-Achse) zerlegt. Dies bedeutet, dass man die ungeordnete Bewegung der Gasteilchen durch eine in 6 Richtungen geordnete Bewegung ersetzen kann. In jede der genannten Richtungen bewegt sich dann  der in dem Würfel enthaltenen Teilchen, so dass auch auf jede Würfelfläche  der Teilchen treffen muss.

Die Anzahl der in dem Würfel befindlichen Teilchen sei N. Unter der Teilchenzahldichte n versteht man den Quotienten aus der Anzahl N der in dem Volumen V enthaltenen Teilchen und dem Volumen.

Der auf eine Fläche A ausgeübte Druck wird allein durch die in der positiven x-Achse fliegenden Teilchen bewirkt. Diese haben natürlich unterschiedliche Geschwindigkeiten. Die Teilchen

                        mit der Geschwindigkeit  haben die Teilchenzahldichte

                        mit der Geschwindigkeit  haben die Teilchenzahldichte  usw.

In einem bestimmten Zeitintervall  kommen aber nicht alle diese Teilchen zum Stoß, sondern nur diejenigen, deren Abstand von der betrachteten Fläche  höchstens

                         usw.

ist. Dies sind diejenigen Teilchen, die sich jeweils in einem Quader mit der Grundfläche A und den Höhen  oder  usw. befinden. Für die Anzahl  dieser Teilchen gilt

                         usw.

Bei dem senkrechten Stoß gegen die Wand werden die Teilchen elastisch reflektiert. Dabei bleiben die Geschwindigkeitsbeträge erhalten. Bezeichnet man die für alle Teilchen als gleich groß vorausgesetzte Masse mit , so beträgt der Impuls eines Teilchens mit der Geschwindigkeit

                        vor dem Stoß               und

                        nach dem Stoß

Da  Teilchen in der Zeit  mit der Geschwindigkeit  gegen die Fläche A stoßen, beträgt also die Impulsänderung dieser Teilchen

Entsprechende Impulsänderungen ergeben sich für die Teilchen mit den Geschwindigkeiten ,  usw.

Für die auf die Fläche A ausgeübten Kräfte gilt dann:

                         usw.

Die Gesamtkraft beträgt also:

Hieraus folgt für den auf die Fläche A ausgeübten Gasdruck

Es ist zweckmäßig, die Quadrate der Einzelgeschwindigkeiten durch einen Mittelwert zu ersetzen, den man als mittleres Geschwindigkeitsquadrat  bezeichnet. Es gilt folgende Definition:

Wenn sich  Teilchen mit der Geschwindigkeit ,  Teilchen mit der Geschwindigkeit  usw. bewegen, so versteht man unter dem mittleren Geschwindigkeitsquadrat  die Größe

wobei  die Gesamtzahl der betrachteten Teilchen ist.

Führt man das mittlere Geschwindigkeitsquadrat in die obige Gleichung für den auf die Fläche A ausgeübten Druck ein und betrachtet weiter, dass sich aus den früher dargelegten Gründen nur  der N Teilchen in Richtung der positiven x-Achse bewegt, so ergibt sich

Da n die Teilchenzahldichte und  die Masse des einzelnen Teilchens bedeuten, gilt für die Gesamtmasse m der in dem Volumen V enthaltenen Teilchen

Hieraus folgt für die Dichte  des Gases

Unter Verwendung dieser Zusammenhänge kann die obige Gleichung für den Druck p auch folgendermaßen geschrieben werden:

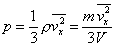                               oder

In vielen Fällen ist es zweckmäßig, dieses Gesetz anders zu schreiben, indem man von der Tatsache Gebrauch macht, dass zu jedem mittleren Geschwindigkeitsquadrat auch eine mittlere kinetische Energie  gehört. Diese beträgt für das einzelne Teilchen

Setzt man diesen Ausdruck in die vorhergehende Gleichung ein und berücksichtigt gleichzeitig, dass für die Gesamtmasse m der in dem Volumen V enthaltenen N Teilchen gilt

so ergibt sich

Wenn es sich um ein abgeschlossenes System handelt, so ist N konstant, aber auch V und T, und damit also auch . Es folgt:

Mit dieser Gleichung haben wir ein wichtiges Gesetz abgeleitet, das auch durch Versuche gefunden werden kann. Es lautet:

Bei einer abgeschlossenen Gasmenge ist bei konstanter Temperatur das Produkt aus dem Volumen V und dem auf die Gefäßwand ausgeübten Druck p konstant.

Die Konstante ist 2/3 des Produktes aus der Gesamtzahl N der in der Gasmenge enthaltenen Teilchen und der mittleren kinetischen Energie  der Teilchen.

Man bezeichnet es als Boyle-Marotte-Gesetz.